Cynthia invests some money in a bank which pays 5% compound interest per year. She wants it to be worth over £8000 at the end of 3 years. What is the smallest amount, to the nearest pound, she can invest?
Question

Answer:
Answer:The smallest amount is [tex]\£6,911[/tex] Step-by-step explanation:we know that The compound interest formula is equal to [tex]A=P(1+\frac{r}{n})^{nt}[/tex] where A is the Final Investment Value P is the Principal amount of money to be invested r is the rate of interest in decimal
t is Number of Time Periods n is the number of times interest is compounded per year
in this problem we have [tex]t=3\ years\\ A=\£8,000\\ r=5\%=5/100=0.05\\n=1[/tex] substitute in the formula above [tex]8,000=P(1+\frac{0.05}{1})^{1*3}[/tex] solve for P[tex]8,000=P(1.05)^{3}[/tex] [tex]P=8,000/(1.05)^{3}[/tex] [tex]P=\£6,910.70[/tex] Round to the nearest pound she can investThe smallest amount is [tex]\£6,911[/tex]
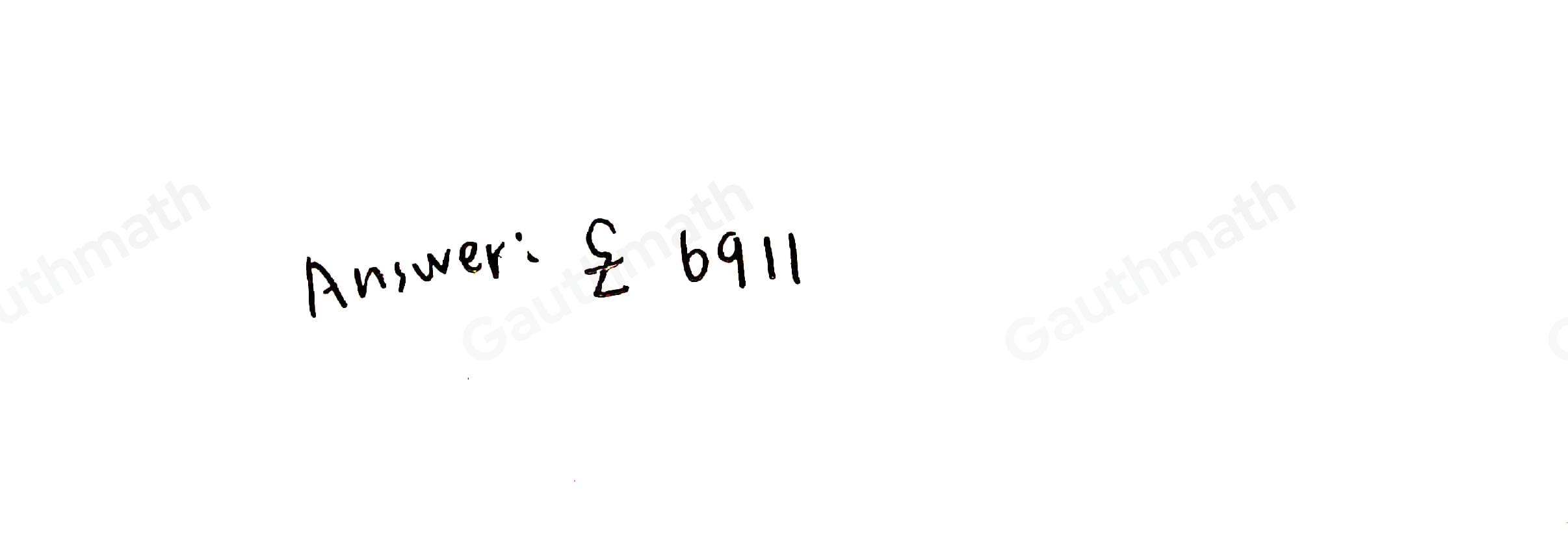
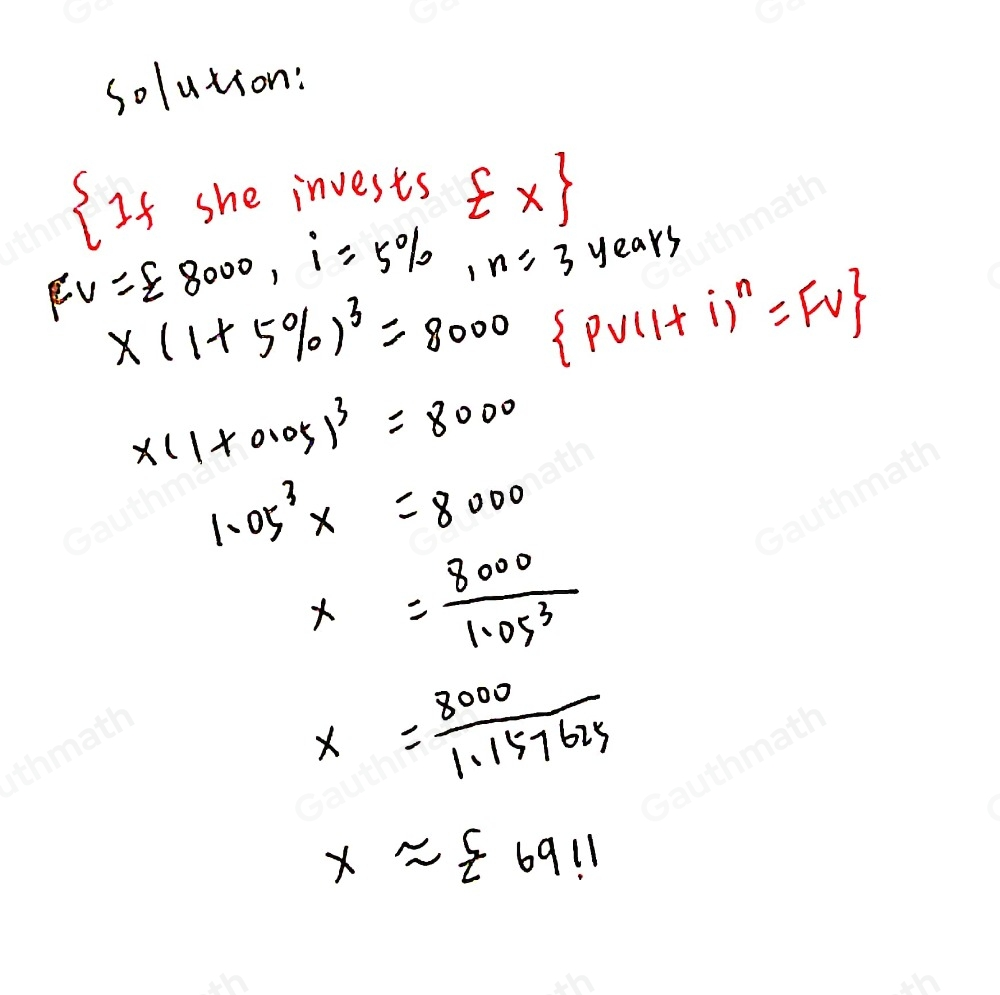
solved
algebra
11 months ago
7362