Which equation can be used to solve for x, the side length of the original square? x2-2x-120=0 x2+2x-120=0 x2-2x+120=0 x2+2x+120=0
Question
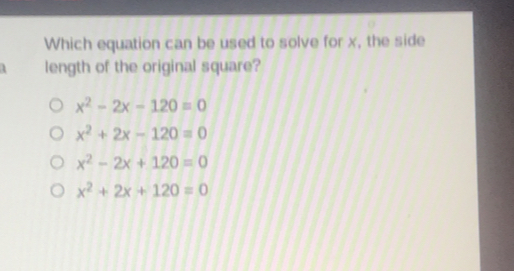
Answer:
Question:A square piece of paper has an area of x2 square units. A rectangular strip with a width of 2 units and a length of x units is cut off of the square piece of paper. The remaining piece of paper has an area of 120 square units.
Which equation can be used to solve for x, the side length of the original square?
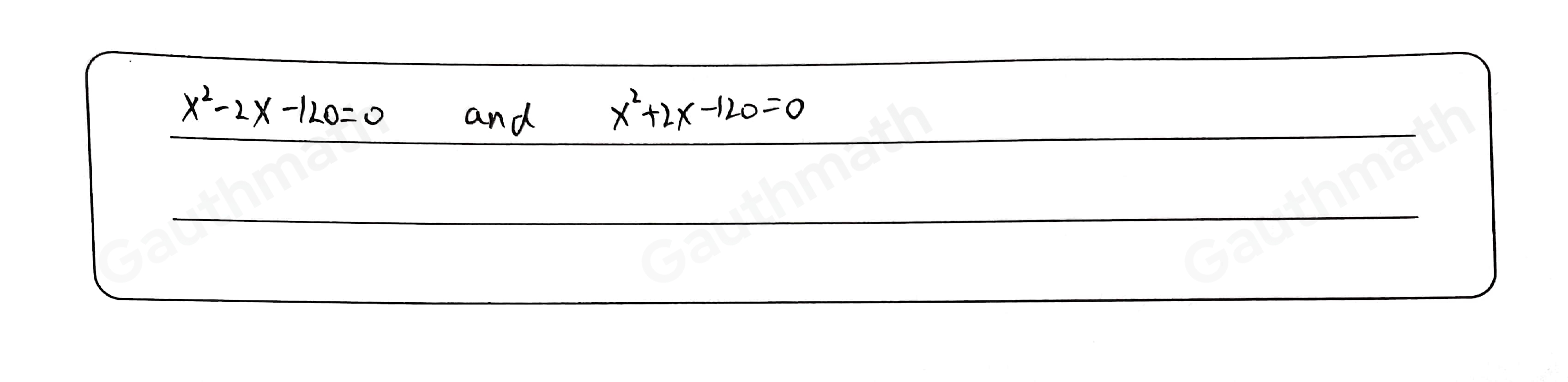
x2 − 2x − 120 = 0
x2 + 2x − 120 = 0
x2 − 2x + 120 = 0
x2 + 2x + 120 = 0Answer:Option a: [tex]x^{2} -2x-120=0[/tex] is the equationExplanation:It is given that the area of the square paper is [tex]x^{2}[/tex] square units.The area of the remaining piece of paper is 120 square units.It is also given that the area of the remaining piece of paper is [tex]x^{2}-2 x[/tex]Thus, equating the area of the remaining piece of paper, we have,[tex]x^{2} -2x=120[/tex]Subtracting 120 from both sides of the equation, we have,[tex]x^{2} -2x-120=0[/tex]Thus, the equation [tex]x^{2} -2x-120=0[/tex] can be used to solve for x.Hence, Option a is the correct answer.

solved
algebra
11 months ago
8330