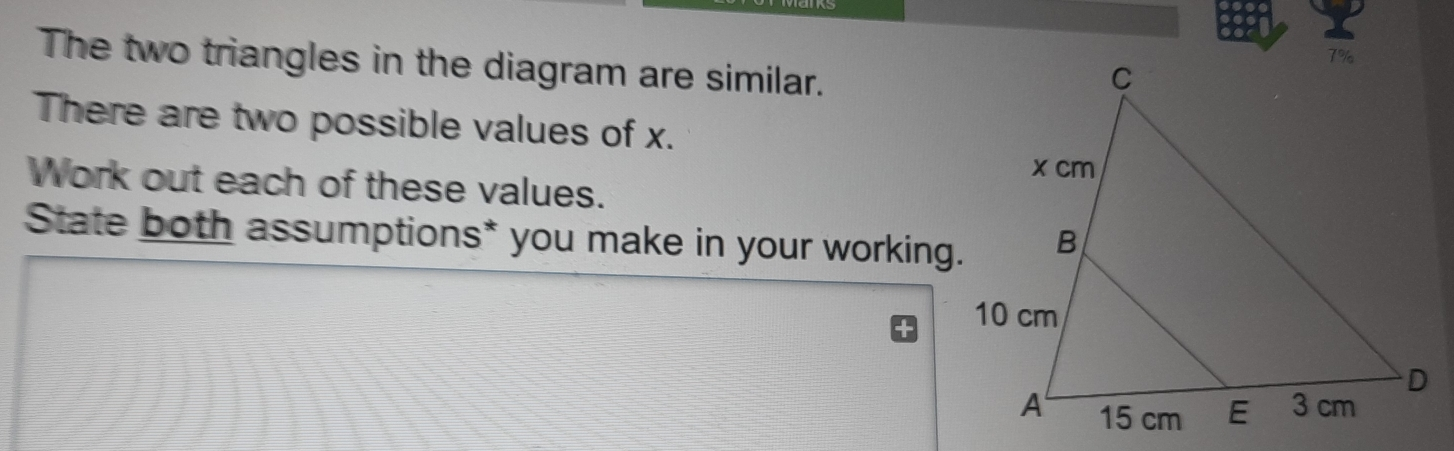
The two triangles in the diagram are similar. There are two possible values of x.. Work out each of these values. State both assumptions* you make in your working.
Question
Answer:
Answer:By changing the order of vertices,We have four conditions,[tex]\triangle ABE\sim \triangle ACD[/tex][tex]\triangle ABE\sim \triangle ADC[/tex][tex]\triangle AEB\sim\triangle ACD[/tex][tex]\triangle AEB \sim \triangle ADC[/tex]When we have [tex]\triangle ABE\sim \triangle ACD[/tex] or [tex]\triangle AEB \sim \triangle ADC[/tex],Then by the property of similar angles,[tex]\frac{AE}{AD}=\frac{AB}{AC}[/tex]⇒ [tex]\frac{15}{18} = \frac{10}{10+x}[/tex]⇒ [tex]150+15x= 180[/tex]⇒ [tex]15x = 180 -150[/tex]⇒ [tex]15x = 30[/tex]⇒ x = 2But, [tex]\triangle ABE\sim \triangle ADC[/tex] or [tex]\triangle AEB\sim\triangle ACD[/tex] is given,Then by the property of similar triangles,[tex]\frac{AB}{AD}=\frac{AE}{AC}[/tex]⇒ [tex]\frac{10}{18} = \frac{15}{10+x}[/tex]⇒ [tex]100+10x= 15\times 18[/tex]⇒ [tex]10x = 270 -100[/tex]⇒ [tex]10x = 170[/tex]⇒ x = 17Note: [tex]\angle A[/tex] is reflexive angle in both triangles this is why, in each condition we took A is corresponding to A.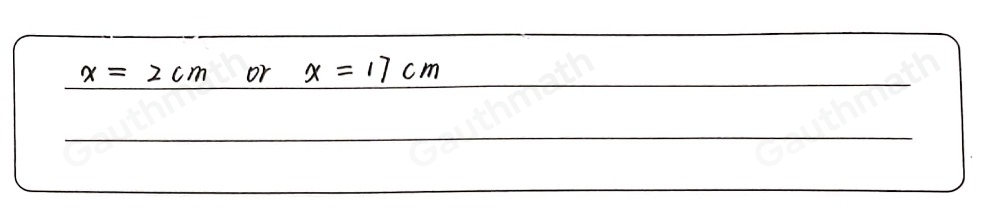

solved
geometry
11 months ago
1466